Selecting the right material for a structure or product requires understanding its mechanical properties, particularly how it responds to different types of forces. Flexural modulus, Young’s modulus, and elastic modulus are three key indicators of a material’s stiffness and deformation behavior. These properties describe how materials respond to forces such as bending, stretching, or compression, and they are widely used in industries like construction, automotive, aerospace, and consumer goods. For example, selecting materials with appropriate modulus values ensures the structural integrity of bridges, the lightweight yet sturdy design of automotive parts, and the durability of electronic device casings. Today, we will explain their definitions, formulas, material values, differences, relationships, and conversions to help guide material selection and design decisions.
1. What is Flexural Modulus?
Before discussing the differences, it is important to first understand each modulus individually. Flexural modulus is widely used in industries where materials experience bending forces, such as in beams, plastic housings, and composite panels.
Flexural modulus measures a material’s resistance to bending. It represents the ratio of stress to strain in the elastic region of a material under flexural loading. This property is particularly useful for evaluating plastics, composites, and thin materials that experience bending rather than direct tension or compression.
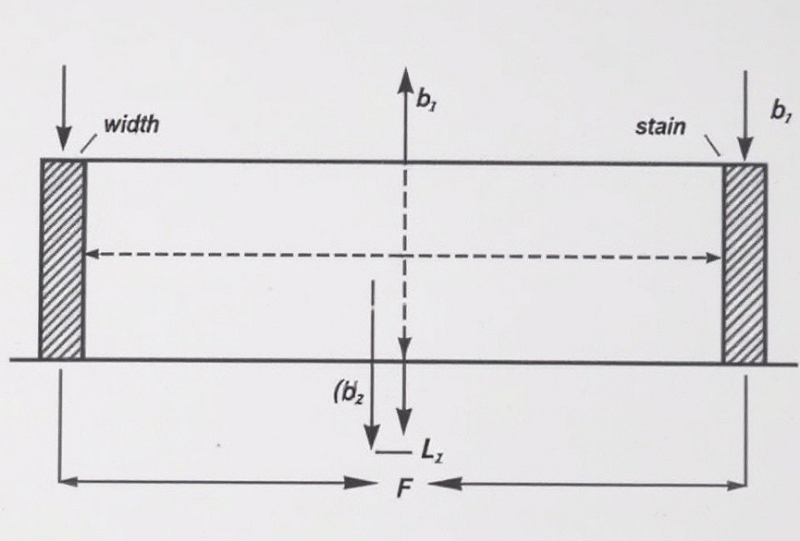
Flexural Modulus Formula & Calculation
Flexural modulus is calculated using the following equation:
Ef = (L³ × m) / (4 × b × d³)
Where:
- Ef = Flexural modulus (MPa or GPa)
- L = Support span (mm)
- m = Slope of the load-deflection curve (N/mm)
- b = Width of the specimen (mm)
- d = Thickness of the specimen (mm)
Flexural modulus is determined using a three-point or four-point bending test, where a material sample is supported at both ends while a force is applied at the center or at two points. The resulting deflection is measured, and the modulus is calculated from the force-deflection relationship.
Flexural Modulus Ratio of Different Plastic & Metal Materials
Different materials have varying bending stiffness, making flexural modulus a key property in material selection for load-bearing components. The values below represent typical flexural modulus ranges for various plastics and metals.
| Material | Flexural Modulus (GPa) |
|---|---|
| Plastics | |
| Polycarbonate (PC) | 2.3 – 2.6 |
| Acrylonitrile Butadiene Styrene (ABS) | 1.9 – 2.3 |
| Polyethylene (PE, HDPE, LDPE) | 0.5 – 1.5 |
| Polypropylene (PP) | 1.2 – 1.5 |
| Polystyrene (PS) | 2.9 – 3.2 |
| Nylon (PA6, PA66) | 2.5 – 3.5 |
| Polyvinyl Chloride (PVC) | 2.4 – 4.5 |
| Polyether Ether Ketone (PEEK) | 3.6 – 4.1 |
| Polyethylene Terephthalate (PET) | 2.0 – 3.0 |
| Metals | |
| Aluminum | 69 |
| Stainless Steel | 193 – 200 |
| Mild Steel | 200 – 210 |
| Titanium | 107 |
| Copper | 110 – 130 |
| Brass | 96 – 110 |
| Magnesium | 44 – 45 |
| Nickel | 200 – 210 |
2. What is Young’s Modulus?
While flexural modulus describes bending stiffness, Young’s modulus is a fundamental property used in structural engineering, material design, and mechanical analysis, where materials are subjected to direct tensile or compressive forces.
Young’s modulus, also called the longitudinal elastic modulus, measures a material’s stiffness under tensile or compressive loads. It defines the proportional relationship between stress and strain within the elastic range of a material.
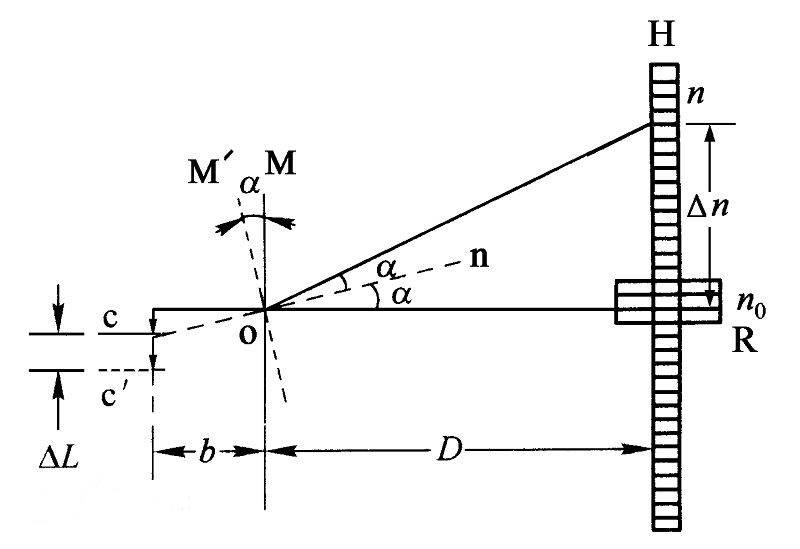
Young’s Modulus Formula & Calculation
Young’s modulus (E) is derived from Hooke’s Law, which states that stress and strain are proportional within the elastic limit:
E = Stress / Strain
Since:
Stress (σ) = Force (F) / Area (A)
Strain (ε) = Change in length (ΔL) / Original length (L)
We can rewrite Young’s modulus as:
E = (F / A) / (ΔL / L)
Where:
- E = Young’s modulus (MPa or GPa)
- σ = Stress (force per unit area, MPa)
- ϵ = Strain (dimensionless, change in length/original length)
To calculate Young’s modulus, a specimen is subjected to a uniaxial tensile force, and the elongation is measured. The modulus is determined from the slope of the initial linear region of the stress-strain curve.
Young’s Modulus Ratio of Different Plastic & Metal Materials
Young’s modulus measures the stiffness of a material when subjected to tensile or compressive forces. It is a key parameter in mechanical and structural engineering, helping to determine how much a material stretches or compresses under load.
| Material | Young’s Modulus (GPa) |
|---|---|
| Plastics | |
| Polycarbonate (PC) | 2.3 – 2.6 |
| Acrylonitrile Butadiene Styrene (ABS) | 1.8 – 2.5 |
| Polyethylene (PE, HDPE, LDPE) | 0.2 – 1.5 |
| Polypropylene (PP) | 1.2 – 1.5 |
| Polystyrene (PS) | 2.9 – 3.2 |
| Nylon (PA6, PA66) | 2.5 – 3.5 |
| Polyvinyl Chloride (PVC) | 2.4 – 4.5 |
| Polyether Ether Ketone (PEEK) | 3.6 – 4.1 |
| Polyethylene Terephthalate (PET) | 2.0 – 3.0 |
| Metals | |
| Aluminum | 69 |
| Stainless Steel | 193 – 200 |
| Mild Steel | 200 – 210 |
| Titanium | 107 |
| Copper | 110 – 130 |
| Brass | 96 – 110 |
| Magnesium | 44 – 45 |
| Nickel | 200 – 210 |
3. What is Elastic Modulus?
So far, we have discussed stiffness under bending and tension. However, materials also resist deformation under other types of stress. The elastic modulus is a broad term that includes different types of stiffness measurements based on the type of force applied.
Elastic modulus is a general term referring to a material’s ability to resist deformation under applied stress. It includes Young’s modulus (tensile/compressive), shear modulus (resistance to shear deformation), and bulk modulus (resistance to uniform compression).
Elastic Modulus Formula & Calculation
Elastic modulus varies depending on the type of stress applied:
Young’s Modulus (Tensile/Compressive)
Young’s modulus (E) is defined as the ratio of stress (σ) to strain (ε):
E = σ / ε
Where:
- E = Young’s modulus (MPa or GPa)
- σ = Stress (MPa)
- ε = Strain (dimensionless)
Shear Modulus (Resistance to Shear Deformation)
Shear modulus (G) is defined as the ratio of shear stress (τ) to shear strain (γ):
G = τ / γ
Where:
- G = Shear modulus (MPa or GPa)
- τ = Shear stress (MPa)
- γ = Shear strain (dimensionless)
Bulk Modulus (Resistance to Volume Change under Pressure)
Bulk modulus (K) is defined as the ratio of applied pressure (p) to the resulting volumetric strain (ΔV/V):
K = p / (ΔV / V)
Where:
- K = Bulk modulus (MPa or GPa)
- p = Applied pressure (MPa)
- ΔV = Change in volume
- V = Original volume
Elastic Modulus Ratio of Different Plastic & Metal Materials
Plastics exhibit a range of elastic modulus values based on their molecular structure and composition. They tend to be more flexible compared to metals. Metals have significantly higher elastic modulus values due to their rigid atomic structures, making them more resistant to deformation under stress.
| Material | Elastic Modulus (GPa) |
|---|---|
| Plastics | |
| Polycarbonate (PC) | 2.3 – 2.6 |
| Acrylonitrile Butadiene Styrene (ABS) | 1.8 – 2.5 |
| Polyethylene (PE, HDPE, LDPE) | 0.2 – 1.5 |
| Polypropylene (PP) | 1.2 – 1.5 |
| Polystyrene (PS) | 2.9 – 3.2 |
| Nylon (PA6, PA66) | 2.5 – 3.5 |
| Polyvinyl Chloride (PVC) | 2.4 – 4.5 |
| Polyether Ether Ketone (PEEK) | 3.6 – 4.1 |
| Polyethylene Terephthalate (PET) | 2.0 – 3.0 |
| Metals | |
| Aluminum | 69 |
| Stainless Steel | 193 – 200 |
| Mild Steel | 200 – 210 |
| Titanium | 107 |
| Copper | 110 – 130 |
| Brass | 96 – 110 |
| Magnesium | 44 – 45 |
| Nickel | 200 – 210 |
4. Flexural Modulus vs Young’s Modulus vs and Elastic Modulus, What is The Difference
As we have introduced each modulus above with details, here we use the below table to sum up the differences between flexural modulus, young’s modulus, and elastic modulus:
| Property | Definition | Measurement Method | Application | Units |
|---|---|---|---|---|
| Flexural Modulus | Measures stiffness in bending | Three-point or four-point bending test | Used for materials subjected to bending loads, such as plastics, composites, and thin sheets | MPa, GPa |
| Young’s Modulus | Measures stiffness under tensile or compressive loading | Tensile or compressive stress-strain test | Used for structural analysis, mechanical design, and material selection | MPa, GPa |
| Elastic Modulus | General term for a material’s resistance to deformation, encompassing Young’s modulus, shear modulus, and bulk modulus | Depends on type: tensile test (Young’s modulus), shear test (shear modulus), compression test (bulk modulus) | Used in engineering and physics to describe overall material stiffness | MPa, GPa |
5. Relationship Between Flexural Modulus, Young’s Modulus, and Elastic Modulus
Although these moduli describe different stiffness properties, they are closely related:
- Flexural Modulus and Young’s Modulus: For isotropic materials, the flexural modulus approximates Young’s modulus. However, for anisotropic materials, such as plastics with additives or composites, the two may differ due to the influence of geometry and material structure.
- Flexural Modulus and Elastic Modulus: Flexural modulus is a subset of elastic modulus, specifically for bending deformation, while elastic modulus encompasses all types of deformation modes.
6. Conversions Between Flexural Modulus, Young’s Modulus, and Elastic Modulus
The relationship between these moduli depends on the material’s isotropy and Poisson’s ratio (ν), which accounts for lateral deformation when a material is stretched or compressed. Below, we show you how to convert flexural modulus to young’s modulus and elastic modulus:
Flexural Modulus (Ef) to Young’s Modulus (E) Conversion
If the elastic modulus refers to Young’s modulus (E), the flexural modulus (Ef) is given by:
Ef = E / (1 – ν²)
Where:
- Ef = Flexural modulus (GPa)
- E = Young’s modulus (GPa)
- ν = Poisson’s ratio (dimensionless)
This equation is used for isotropic materials where bending stiffness is related to tensile stiffness.
Shear Modulus (G) to Young’s Modulus (E) Conversion
If the elastic modulus refers to shear modulus (G), the relationship is:
G = E / [2(1 + ν)]
Where:
- G = Shear modulus (GPa)
- E = Young’s modulus (GPa)
- ν = Poisson’s ratio
This equation describes how a material resists shearing deformation in response to applied forces.
Bulk Modulus (K) to Young’s Modulus (E) Conversion
If the elastic modulus refers to bulk modulus (K), the relationship is:
K = E / [3(1 – 2ν)]
Where:
- K = Bulk modulus (GPa)
- E = Young’s modulus (GPa)
- ν = Poisson’s ratio
This equation is used to determine a material’s resistance to uniform compression.
Flexural Modulus (Ef) to Shear Modulus (G) Conversion
The relationship between flexural modulus (Ef) and shear modulus (G) is derived using Young’s modulus (E) as an intermediary:
Step 1: Convert Flexural Modulus (Ef) to Young’s Modulus (E)
For isotropic materials:
Ef = E / (1 – ν²)
Rearranging for E:
E = Ef × (1 – ν²)
Step 2: Convert Young’s Modulus (E) to Shear Modulus (G)
Using the shear modulus equation:
G = E / [2(1 + ν)]
Substituting E = Ef × (1 – ν²):
G = [Ef × (1 – ν²)] / [2(1 + ν)]
Final Conversion Formula:
G = (Ef × (1 – ν²)) / [2(1 + ν)]
Flexural Modulus (Ef) to Bulk Modulus (K) Conversion
To relate flexural modulus (Ef) to bulk modulus (K), we use Young’s modulus (E) as an intermediary.
Step 1: Convert Flexural Modulus (Ef) to Young’s Modulus (E)
As before:
E = Ef × (1 – ν²)
Step 2: Convert Young’s Modulus (E) to Bulk Modulus (K)
Using the bulk modulus equation:
K = E / [3(1 – 2ν)]
Substituting E = Ef × (1 – ν²):
K = [Ef × (1 – ν²)] / [3(1 – 2ν)]
Final Conversion Formula:
K = (Ef × (1 – ν²)) / [3(1 – 2ν)]
7. FAQs
Is Flexural Modulus the Same as Elastic Modulus?
No, flexural modulus is not the same as elastic modulus. Elastic modulus is a general term that includes Young’s modulus, shear modulus, and bulk modulus. Flexural modulus specifically describes stiffness in bending and is influenced by material geometry and load distribution.
Is Flexural Modulus the Same as Young’s Modulus?
No, flexural modulus is not the same as Young’s modulus, though they are related. Young’s modulus measures stiffness under direct tensile or compressive forces, while flexural modulus measures stiffness in bending. For many isotropic materials, flexural modulus is slightly higher than Young’s modulus due to the effects of Poisson’s ratio and stress distribution in bending.
Is Young’s Modulus the Same as Elastic Modulus?
Young’s modulus is a type of elastic modulus, but not the only one. Elastic modulus is a broad term that includes:
- Young’s modulus (tensile/compressive stiffness)
- Shear modulus (resistance to shear deformation)
- Bulk modulus (resistance to uniform compression)
Young’s modulus specifically applies to axial deformations, while elastic modulus can refer to multiple types of deformation resistance.

