In the meticulously detailed world of die casting and mold manufacturing, understanding the mechanical properties of materials is crucial. Among these properties, Shear Modulus and Young’s Modulus stand prominent, serving as fundamental indicators of a material’s elasticity under different types of stress. This article from diecasting-mould.com delves into the definitions, differences, and applications of Shear Modulus and Young’s Modulus in the die-casting industry.
About Shear Modulus
Shear Modulus, also known as the modulus of rigidity, denotes a material’s response to shear stress. It is the ratio of shear stress to the shear strain, providing a measure of a material’s rigidity. In other words, it quantifies how a material deforms transversally when a force is applied parallel to one of its surfaces while the opposite surface is held fixed. Its formula is given by:
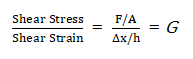
where:
- G is the Shear Modulus,
- F is the force applied,
- A is the area,
- Δx is the transverse displacement,
- h is the height from the fixed layer.
Metals used in die casting, such as aluminum and zinc alloys, have specific shear moduli that dictate their resistance to shearing forces during the molding process.
About Young’s Modulus
Young’s Modulus, or the modulus of elasticity, measures a material’s stiffness by quantifying the linear relationship between tensile (or compressive) stress and strain. It reflects how a material stretches or compresses along an axis when opposing forces are applied. The formula for Young’s Modulus is:
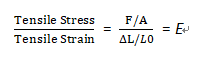
where:
- E is the Young’s Modulus,
- F is the force applied,
- A is the cross-sectional area,
- ΔL is the change in length,
- L0 is the original length.
The Young’s Modulus of aluminum alloys and zinc, frequently used in die casting at Junying, is a critical factor for the engineers in determining how these materials will behave under tensile or compressive loads during service.
Shear Modulus vs Young’s Modulus: The Key Differences
The primary difference between the Shear Modulus and Young’s Modulus lies in the type of deformation they describe. Shear Modulus is concerned with the deformation due to forces applied parallel to a material’s surface, causing it to shear. In contrast, Young’s Modulus pertains to deformation due to forces applied perpendicularly to a material’s surface, causing it to stretch or compress.
Application in Die Casting: Which One to Use?
In die casting, both the Shear Modulus and Young’s Modulus are vital for ensuring the integrity and functionality of the final product.
- -Material Selection
In die casting, aluminum and zinc are commonly used materials, each with distinct Shear and Young’s Moduli. When selecting a material, both moduli must be taken into account to predict how the material will behave under the stresses experienced during and after casting.
- -Mold Design
Mold design must consider the Shear and Young’s Moduli of the material to prevent defects such as warping or distortion. For instance, a material with a low Shear Modulus might deform under the high shear stresses during mold release.
- -Quality Control
Quality control processes in die casting can involve testing the Shear and Young’s Moduli to ensure that the material properties match the specifications required for the intended application.
- -Structural Integrity
The structural integrity of a die-cast part under operational stresses can be assessed using both moduli. For example, parts expected to experience significant shear forces would benefit from a material with a high Shear Modulus.
- -Performance Prediction
Predicting the performance of die-cast parts often involves calculations using Young’s Modulus, especially for components that are subjected to tensile or compressive forces during their service life.
The Shear Modulus of Some Other Common Materials
The shear modulus, also known as the modulus of rigidity, represents how a material deforms under shear stress. It measures the material’s stiffness and is given by the ratio of shear stress to shear strain. Different materials have varying shear moduli, and this property plays a key role in determining how a material will behave when subjected to shear forces. Below are the approximate shear moduli for some common materials:
- – Steel: 79.3 GPa (Gigapascals)
- – Aluminum: 25.5 GPa
- -Titanium: 41.4 GPa
- – Copper: 44.7 GPa
- -Brass: 35.5 GPa
- -Nickel: 76.0 GPa
- -Cast Iron: 44.5 GPa
- -Glass: 26.2 GPa
- -Concrete: 9.7–17.2 GPa (varying with the type and composition)
- -Wood: 1–1.6 GPa (varies with species, grain orientation, and moisture content)
- -Polymers: 0.01–1.5 GPa (highly variable depending on the type of polymer and its processing)

