Materials science relies heavily on the concepts of stress and strain. Stress refers to the forces applied to a material, while strain describes the resulting deformation. Though related, these two terms have distinct meanings and applications. This article will explain the key differences between stress and strain and why they matter for materials engineering.
What is Stress?
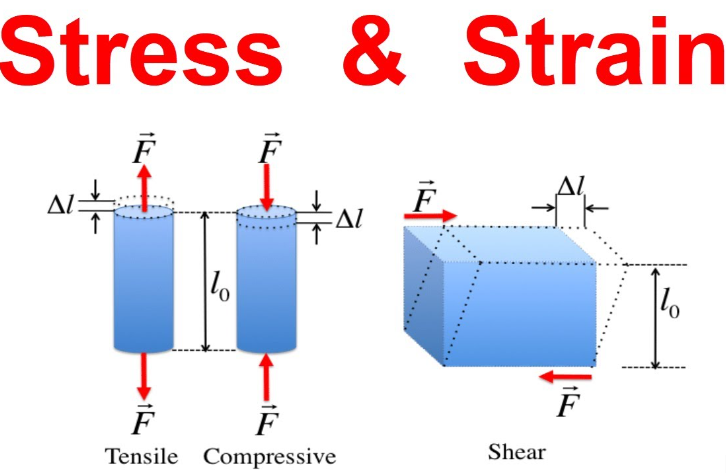
Stress is defined as the force per unit area acting on a material. It is caused by external forces that pull, push, twist or shear the material. The common types of stresses are tensile, compressive, shear, and torsional stress. Stress is calculated by dividing the applied force (F) by the cross-sectional area (A) it acts on:
- Stress = F/A
Stress causes materials to deform. At low levels, the deformation is elastic and reversible. But high stresses can cause permanent plastic deformation or even fracture. Understanding a material’s stress response is crucial for proper design and material selection.
What is Strain?
Strain describes the deformation that occurs in a material under stress. It measures the change in shape and dimensions produced by applied forces. Strain is calculated as the change in length (∆L) divided by the original length (L0):
- Strain = ∆L/L0
Strains can be tensile, compressive, or shear, matching the type of applied stress. The strain response depends on the material and stress level. At low stresses, strain is elastic, and the material returns to its original shape when stress is removed. At higher stresses, permanent plastic strain occurs.
Key Differences Between Stress and Strain
Understanding the nuanced difference between stress and strain is foundational in materials science and structural engineering. Analyzing both reveals insights into material behavior that inform critical design decisions. Their relationship also allows the calculation of key mechanical properties. Mastering stress and strain principles is crucial for engineers across many fields.
| Property | Stress | Strain |
| Definition | Force per unit area applied to a material | Deformation or change in dimensions caused by stress |
| Symbol | σ | ε |
| Units | Pascals (Pa), psi | Dimensionless or % |
| Type | Tensile, compressive, shear, torsional | Tensile, compressive, shear, volumetric |
| Cause | External forces | Deformation due to applied stress |
| Effect | Deforms material, changes properties | Elastic deformation or permanent plastic deformation |
| Behavior | Reversible (elastic) or permanent (plastic) | Recoverable (elastic) or permanent (plastic) |
| Failure | Fracture if stress exceeds strength | Fracture if strain exceeds ductility |
| Calculation | Stress = Force / Area | Strain = (Change in length) / (Original length) |
| Measurement | Load cells, strain gauges | Extensometers, strain gauges |
| Related Properties | Young’s modulus, shear modulus | Poisson’s ratio, ductility |
Examples of Stress and Strain of Different Materials
- Metals:
– Ductile metals like aluminum and copper yield and deform plastically under tensile stress. Their stress-strain curves show elastic deformation followed by plastic flow.
– Brittle metals like cast iron fracture with minimal plastic deformation. Their stress-strain curves are linear until sudden fracture.
– Steel displays an elastic region, yield point, strain hardening, and ultimate tensile strength before fracture.
- Polymers:
– Rigid polymers like PMMA experience linear elastic deformation followed by brittle fracture.
– Ductile polymers like polyethylene undergoes elastic deformation, yielding, necking, and drawing before failure.
– Elastomers like rubber display extreme elastic deformation with minimal plastic flow. Their stress-strain curves are nonlinear.
- Ceramics:
– Most ceramics are brittle, showing elastic deformation and sudden fracture with no plastic flow. Their stress-strain curves are linear.
– Some ceramics are semi-brittle, exhibiting some non-linear behavior and microcracking.
- Composites:
– Fiber-reinforced composites typically display linear elastic behavior followed by fiber breakage and plastic matrix deformation.
– Response depends on fiber type (glass, carbon) and matrix material (polymer, metal, ceramic).
- Concrete:
– Concrete shows an initial elastic region, followed by microcracking and plastic deformation before fracture. Stress-strain curves are nonlinear.
- Wood:
– Wood exhibits an initial elastic region, yield point, and plastic deformation with ductile splintering failure parallel to grain direction.

